求外心 (Circumcentre)坐標的方法

求取三角形的外心並沒有簡單公式可用。如果該三角形的三條邊都不是水平線或垂直線，就只能從最基本定義入手，就是找當中兩條邊的垂直平分線 (Perpendicular Bisector)。然後用聯立方程的方法找其交點，亦即是外心的坐標。

例子: 求 △ABC 的外心坐標 (Circumcentre)

Step 1) 求 AB 的垂直平分線的方程:

\begin{align*}
m_{AB} &= \frac{1-3}{1-6}\\
&= \frac{2}{5}
\end{align*}

$$\begin{align*}
\text{Mid-point of AB} &= \Big (\frac{1+6}{2},\frac{1+3}{2}\Big )\\
&= \Big (\frac{7}{2},2\Big )
\end{align*}$$

Equation of perpendicular bisector of AB 
AB 的垂直平分線的方程
$$\begin{align*}
y-2 &= \frac{-1}{\frac{2}{5}}(x-\frac{7}{2})\\[4pt] y-2 &= \frac{-5}{2}(x-\frac{7}{2})\\
2y-4 &= -5x + \frac{35}{2}\\
5x+2y&=4+\frac{35}{2}\\
10x+4y&=43\ …(1)
\end{align*}$$

Step 2) 用相同方法求 AC 的垂直平分線的方程:

$$2x+8y=27\ …(2)$$

Step 3) 解聯立方程
$$\begin{cases} 10x+4y &= 43 \\ 2x + 8y &= 27 \end{cases}$$

$$ x=\frac{59}{18},\ y=\frac{23}{9}$$

△ABC 的外心 = ##\big ( \large \frac{59}{18} \normalsize,\large \frac{23}{9} \normalsize \big )##

---

但如果三角形的其中一條邊是水平線或垂直線，情況會便得較簡單。

例子: 求 △ABC 的外心坐標 (Circumcentre)

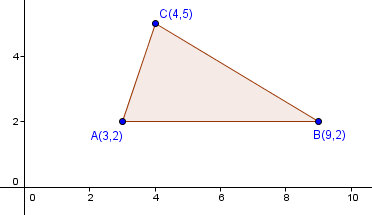
由於線段AB是水平線，其垂直平分線 (perpendicular bisector) 可輕易求得。

$$\begin{align*}
x &= \frac{3+9}{2}\\[4pt] x &= 6
\end{align*}$$

△ABC 的外心必定在 x=6 這直線上，換句話說，其 x坐標=6。由於三角形的外心亦是其外接圓(circumcircle)的圓心，基於這性質，我們知道外心和三角形的頂點的距離相等，該距離亦即是圓形半徑長度。由此可求得外心的 y坐標。

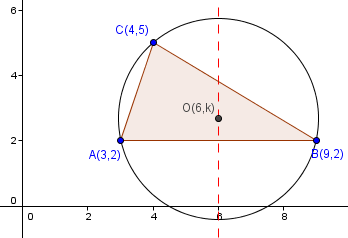
Let the coordinates of circumcentre be O(6,k).
設外心坐標為 O(6,k)

$$\begin{align*}
OA &= OC\\
\sqrt{(3-6)^2+(2-k)^2} &= \sqrt{(4-6)^2+(5-k)^2}\\
9 + 4 -4k + k^2 &= 4 + 25 -10k +k^2\\
13 -4k &= 29 – 10k\\
6k &= 16\\
k &=\frac{8}{3}
\end{align*}$$

△ABC 的外心 = ##\big (6,\large \frac{8}{3} \normalsize \big )##

標籤: circumcenter, circumcentre, 外心

分類: 幾何、坐標及三角學