求形心 (Centroid)坐標的方法

還顧舊試題的內容，形心 (Centroid) 是較少出現在試題中。雖然如此，我們亦應該了解形心的性質而及找其坐標的方法。

形心(Centroid)性質

1) 中線 (Median) 把三角形分成兩個小三角形。而這兩個三角形的面積相同。

2) 形心(Centroid)把各條中線(Median)分成兩段。而線段的長度比是 1:2。

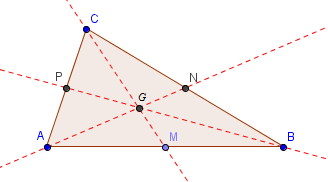
即是
$$\begin{align*}
MG:GC &= 1:2\\
NG:GA &= 1:2\\
PG:GB &= 1:2
\end{align*}$$

證明:

參考下圖， P點和 N點分別是 AC 及 BC 的中點(mid-point)。根據中點定理 (Mid-point theorem)， ##PN // AB## 及 ##PN=\frac{1}{2}AB##

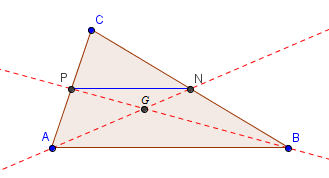
由此，我們可以證明 △GNP ~ △GAB

$$\begin{align*}
\therefore \frac{NG}{GA}&=\frac{PG}{GB}=\frac{PN}{AB}\\[4pt] \frac{NG}{GA}&=\frac{PG}{GB}=\frac{1}{2}\\
\end{align*}$$

而 MG:GC=1:2 亦可用相同的方法來證明。

3) 形心坐標公式

設三角形頂點坐標為 ##(x_{\small A},y_{\small A})##，##(x_{\small B},y_{\small B})## 及 ##(x_{\small C},y_{\small C})##

$$G=\Big(\frac{x_{\small A}+x_{\small B}+x_{\small C}}{3},\frac{y_{\small A}+y_{\small B}+y_{\small C}}{3}\Big)$$

證明:

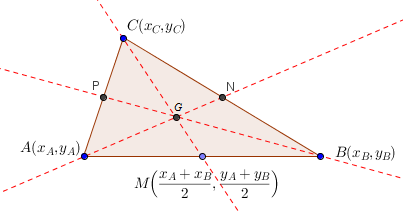
設 M 點是 AB 的中點(mid-point)

$$\therefore M=\Big(\frac{x_{\small A}+x_{\small B}}{2},\frac{y_{\small A}+y_{\small B}}{2}\Big)$$

已知 ##MG:GC = 1:2##

運用分點公式
Using section formula,

$$\begin{align*}
G &= \Big(\frac{2 \cdot \frac{x_{\small A}+x_{\small B}}{2}+1 \cdot x_{\small C}}{1+2},\frac{2 \cdot \frac{y_{\small A}+y_{\small B}}{2}+1 \cdot y_{\small C}}{1+2}\Big)\\[4pt] &=\Big(\frac{x_{\small A}+x_{\small B}+x_{\small C}}{3},\frac{y_{\small A}+y_{\small B}+y_{\small C}}{3}\Big)
\end{align*}$$

標籤: centroid, 形心

分類: 幾何、坐標及三角學