求內心 (Incentre)坐標的方法

在坐標平面上找三角形的內心(Incentre)的坐標絕不容易。但原來找內心是有公式的，只是我們的課程沒有教授這公式。

內心公式

參考下圖， a,b及c 分別是三角形的邊長，而 I 點是三形的內心。

內心(Incentre)坐標:

$$I=\Big (\frac{a\cdot x_a+b\cdot x_b+c\cdot x_c}{a+b+c},\frac{a\cdot y_a+b\cdot y_b+c\cdot y_c}{a+b+c}\Big )$$

驟眼看此公式似乎很複雜，但其實很簡單。分子每一項都是三角形的頂點的坐標和其對邊長度相乘。而分母就是三角形的周界。只要練習一兩次，便能記住這公式。

例題

已知三點 A(2, 1), B(2, 3) 及 C(6, 3)，求 ΔABC 的內心(incentre)的坐標。

題解:

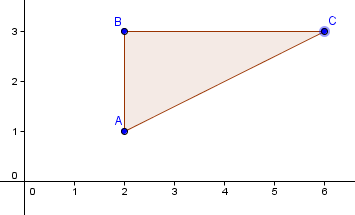
$$\begin{align*}
AB &= 2\\
BC &= 4\\
AC &= \sqrt{(6-2)^2 + (3-1)^2}\\
&=\sqrt{20}
\end{align*}$$

內心 x坐標:
x coordinate of incentre:
$$\begin{align*}
&\frac{4\cdot 2+\sqrt{20}\cdot 2+2 \cdot 6}{2+4+\sqrt{20}}\\[4pt] =&\frac{20+2\sqrt{20}}{6+\sqrt{20}}\\[4pt] =&\frac{20+2\sqrt{20}}{6+\sqrt{20}} \cdot \frac{6-\sqrt{20}}{6-\sqrt{20}}\\[4pt] =&\frac{120-20\sqrt{20}+12\sqrt{20}-40}{36-20}\\[4pt] =&\frac{80-8\sqrt{20}}{16}\\[4pt] =&\frac{80-16\sqrt{5}}{16}\\[4pt] =&5-\sqrt{5}
\end{align*}$$

內心 y坐標:
y coordinate of incentre:
$$\begin{align*}
&\frac{4\cdot 1+\sqrt{20}\cdot 3+2 \cdot 3}{2+4+\sqrt{20}}\\[4pt] =&\frac{10+3\sqrt{20}}{6+\sqrt{20}}\\[4pt] =&\frac{10+3\sqrt{20}}{6+\sqrt{20}} \cdot \frac{6-\sqrt{20}}{6-\sqrt{20}}\\[4pt] =&\frac{60-10\sqrt{20}+18\sqrt{20}-60}{36-20}\\[4pt] =&\frac{8\sqrt{20}}{16}\\[4pt] =&\frac{16\sqrt{5}}{16}\\[4pt] =&\sqrt{5}
\end{align*}$$

內心坐標 = ##(5-\sqrt{5},\sqrt{5})##

證明 Proof

求內心的公式，我們須要用上角平分線 (Angle Bisector)的一個性質，大家可先看另文《角平分線(Angle Bisector)的秘密》，然後再繼續。

由於 x 坐標和 y 坐標的處理方法完全相同，以下只列出 x 坐標的計算。參考下圖，紅線是三角形的角平分線 (Angle Bisector)，I點是三角形的內心(Incentre)。而紅線和 BC相交於 D點。

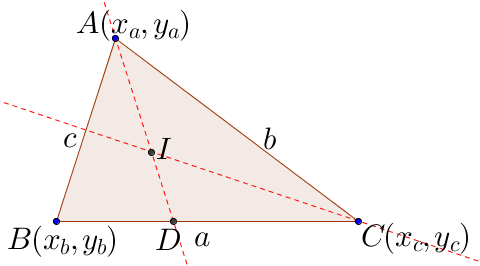
第一步: 找 D點坐標

運用分點公式
Using section formula,

第二步: 求 CD 長度

第三步: 找 I點坐標

集中看 ΔADC。由於 CI 同樣是該三角形的角平分線。

$$\begin{align*}
\therefore AI:ID &= AC: CD\\
&= b:\frac{ab}{b+c}
\end{align*}$$

運用分點公式
Using section formula,

$$\begin{align*}
x_{\small I} &= \frac{CD \cdot x_a + AC \cdot x_{\small D}}{AC+CD}\\[4pt] &=\frac{\frac{ab}{b+c}\cdot x_a + b \cdot \frac{b \cdot x_b + c \cdot x_c}{b+c}}{b+\frac{ab}{b+c}}\\[4pt] &= \frac{ab \cdot x_a + b \cdot (b\cdot x_b + c \cdot x_c)}{b(b+c)+ab}\\[4pt] &=\frac{b(a \cdot x_a + b\cdot x_b + c \cdot x_c)}{b(a+b+c)}\\[4pt] &=\frac{a \cdot x_a + b\cdot x_b + c \cdot x_c}{a+b+c}
\end{align*}$$

而 y坐標的處理方法完全一樣。

總結

在坐標平面上找三角形的內心坐標並不容易。只要運用此公式，便能相對容易地找到內心的坐標。但由於公式涉及三角形的邊長，而這些邊長大都只能以根式 (surd form)表示，所以化簡其結果時的步驟會較多。

相關試題

• 2006P2Q48

標籤: incenter, incentre, 內心

分類: 幾何、坐標及三角學