HKDSE 2024 Maths Paper II 題解

方法一：

方法二：

$$\begin{align*}
&\ \frac{(2\alpha)^3}{(4\alpha^{-5})^{-1}}\\[2pt] =&\ \frac{8\alpha^3}{4^{-1}\alpha^5}\\[2pt] =&\ \frac{4 \times 8\alpha^3}{\alpha^5}\\[2pt] =&\ \frac{32}{\alpha^2}
\end{align*}$$

$$\begin{align*}
k &= \frac{5}{2m} +n\\[2pt] k -n &= \frac{5}{2m}\\[2pt] m &= \frac{5}{2(k -n)}
\end{align*}$$

$$\sqrt{333}=18.24828759$$

A 是正確。以下列出各選項的正確近似值。

設一個蘋果和一個檸檬的售價分別為 x 及 y。
Let the price of an apple and a lemon be x and y respectively.

$$\begin{cases}
2x +3y = 38\\
3x + 2y = 47
\end{cases}$$

解聯立方程
Solving the equations,

$$x = 13, y=4$$

$$\begin{align*}
&\ 4x + 7y\\
=&\ 4(13) ＋7(4)\\
=&\ $80
\end{align*}$$

$$\begin{align*}
4x^2 +2ax +3a &\equiv x(4x +b) +2c\\
4x^2 \color{red}{+2ax} \color{blue}{+3a} &\equiv 4x^2 \color{red}{+bx} \color{blue}{+2c}
\end{align*}$$

比較係數
Comparing the coefficients,
$$\begin{align*}
2a &= b\\
\frac{a}{b} &= \frac{1}{2}\\
a:b &= 1:2\\[6pt] 3a &=2c\\
\frac{a}{c} &= \frac{2}{3}\\
a:c &= 2:3
\end{align*}$$

$$\begin{eqnarray}
a &: &b &\ &= 1 &: &2 &\ \\
a &\ &\ &:c &= 2 &\ &\ &:3 \\
\end{eqnarray}$$

$$\begin{eqnarray}
a &: &b &\ &= 2 &: &4 &\ \\
a &\ &\ &:c &= 2 &\ &\ &:3 \\
\hline{}
a &: &b &: c &= 2 &: &4 &:3 \\
\end{eqnarray}$$

方法一：因式分解 Factorization
$$\begin{align*}
x^2 -3x &= (m -1)^2 -3(m -1)\\
x^2 -(m -1)^2 &= 3x -3(m -1)\\
\big(x +(m -1)\big)\big(x -(m -1)\big) &= 3x -3m +3\\
(x +m -1)(x -m +1) &= 3(x -m +1)\\
(x +m -1)\color{red}{(x -m +1)} -3\color{red}{(x -m +1)} &= 0\\
\color{red}{(x -m +1)}(x +m -1 -3) &= 0\\
(x -m +1)(x +m -4) &= 0\\
x -m +1 = 0\ \ \text{or}\ \ x +m -4 &= 0\\
x = m -1\ \ \text{or}\ \ x &= 4 -m
\end{align*}$$

方法二：
把各選項中的解代入方程，如果左方和右方相等，該解為正確。
$$\begin{align*}
x^2 -3x &= (m -1)^2 -3(m -1)\\
x^2 -3x &= m^2 -2m +1 -3m +3\\
x^2 -3x &= m^2 -5m +4
\end{align*}$$

當 x = m − 1,
$$\begin{align*}
\text{LHS 左方} &= (m -1)^2 -3(m -1)\\
&= m^2 -2m +1 -3m +3\\
&= m^2 -5m +4\\
&=\text{RHS 右方}
\end{align*}$$

因此 x = m − 1 為方程的解，並可排除選項 C 及 D。

當 x = m − 4,
$$\begin{align*}
\text{LHS 左方} &= (m -4)^2 -3(m -4)\\
&= m^2 -8m +16 -3m +12\\
&= m^2 -11m +28\\
&\neq\text{RHS 右方}
\end{align*}$$

因此 x = m − 4 並不是方程的解，亦可排除選項 A。

當 x = 4 − m,
$$\begin{align*}
\text{LHS 左方} &= (4 -m)^2 -3(4 -m)\\
&= 16 -8m +m^2 -12 +3m\\
&= m^2 -5m +4\\
&=\text{RHS 右方}
\end{align*}$$

因此 x = 4 − m 為方程的解，所以答案為 B

$$\begin{align*}
g(1) &= g(2)\\
(1 +1)(1 +a) &= (2 +1)(2 +a)\\
2(1 +a) &= 3(2+a)\\
2 +2a &= 6 +3a\\
2 -6 &= 3a -2a\\
a &= -4\\[8pt] \end{align*}$$

$$ \therefore g(x) = (x +1)(x -4)\\[10pt] \begin{align*}
g(a) &= g(-4)\\
&= (-4 +1)(-4 -4)\\
&= (-3)(-8)\\
&= 24
\end{align*}$$

f(x) 可被 x + k 整除
f(x) is divisible by x + k.
∴ f(−k)=0

$$\begin{align*}
f(-k) &= 0\\
(-k)^3 +k(-k)^2 +5(-k) +10 &= 0\\
-k^3 +k^3 -5k +10 &= 0\\
k &= 2
\end{align*}$$

$$\begin{align*}
&\ \text{remainder 餘式}\\
=&\ f(-1)\\
=&\ (-1)^3 +2(-1)^2 +5(-1) + 10\\
=&\ -1 +2 -5 +10\\
=&\ 6
\end{align*}$$

$$
\begin{align*}
\frac{1 -x}{2} &\ge 4 & \text{or}&\ & 7 +5x &\le -3\\
1 -x &\ge 8 & \text{or}&\ & 5x &\le -10\\
-x &\ge 7 & \text{or}&\ & x &\le -2\\
x &\le -7 & \text{or}&\ & x &\le -2\\
\end{align*}\\
\ \\
\therefore x \le -2$$

設全校學生總數為 N。
Let the total number of students be N.
$$\begin{align*}
N \times 40\% &= N \times 40\% \times \beta \% + N \times 60\% \times 30\%\\
0.4 &= 0.4 \times \beta \% +0.18\\
0.22 &= 0.4 \times \beta \%\\
0.22 \div 0.4 &= \beta \%\\
\beta \% &= 0.55\\
\beta \% &= 55\%
\end{align*}$$

$$\text{平均速率}= \frac{\text{總行走距離}}{\text{總花費時間}}\\[2pt] \text{Average Speed}= \frac{\text{Total distance travelled}}{\text{Total Time Spent}}$$

$$\begin{align*}
&\ \text{總行走距離 Total distance travelled}\\
=&\ 60 \times \frac{18}{60} +40 \times \frac{27}{60}\\[2pt] =&\ 36\,\text{km}
\end{align*}$$ $$
\begin{align*}
&\ \text{平均速率 Average speed}\\[2pt] =&\ \frac{36\,\text{km}}{\frac{18+27}{60}\text{h}}\\[2pt] =&\ 48\,\text{km/h}
\end{align*}$$

$$\begin{align*}
\text{Let 設}\ z &=\frac{kx^2}{y}\\
\end{align*}$$

   z的新值 New Value of z 

   百份數變化 Percentage Change

相關文章: 變分與百分數變化 Variation and Percentage Change

$$\begin{align*}
y &= 2(6 -x)^2 -7\\
&= 2(36 -12x +x^2) -7\\
&= 72 -24x +2x^2 -7\\
&= 2x^2 -24x +65
\end{align*}$$

A)
##x^2## 的係數為正數，即是圖像開口向上。
The coefficient of ##x^2## is positive. Thus, the graph opens upwards.

因此選項 A 為正確答案。

B)
當 ##y=0##,
$$\begin{align*}
2x^2 -24x +65 &= 0\\
x=4.13\ \text{or}\ x&=7.87
\end{align*}$$

因此選項 B 錯誤。

C)
## y = 2x^2 -24x +65##

所以 y-截距 y-intercept = 65。

因此選項 C 錯誤。

D)
當 ##x=-6##
$$\begin{align*}
y &= 2\big(6-(-6)\big)^2 -7\\
&= 281\\
&\neq -7
\end{align*}$$

因此選項 D 錯誤。

$$\begin{cases}
2 \pi r \times \frac{\theta}{360\deg} = 8\pi\ ..(1)\\
\pi r^2 \times \frac{\theta}{360\deg} = 80\pi\ ..(2)
\end{cases}$$ $$
(2) \div (1)\\
\begin{align*}
\frac{\pi r^2 \times \frac{\theta}{360\deg}}{2 \pi r \times \frac{\theta}{360\deg}} &= \frac{80\pi}{8\pi}\\[2pt] \frac{r}{2} &= 10\\[2pt] r &= 20
\end{align*}$$

把 ##r=20## 代入 (1)

參考下圖，

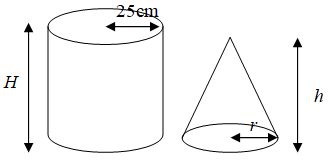
$$\begin{align*}
\frac{H}{h} &= \frac{32}{15}\\[12pt] \frac{\pi(25)^2H}{\frac{1}{3}\pi r^2h} &= \frac{10}{9}\\[2pt] \frac{25^2H}{\frac{1}{3}r^2h} &= \frac{10}{9}\\[2pt] \frac{625H}{r^2h} &= \frac{10}{9} \times \frac{1}{3}\\[2pt] \frac{625}{r^2} \times \frac{32}{15} &= \frac{10}{27}\ \Big(\because\frac{H}{h} = \frac{32}{15}\Big)\\[2pt] \frac{1}{r^2} &= \frac{1}{3600}\\[2pt] r^2 &= 3600\\[2pt] r &= 60\,\text{cm}
\end{align*}$$

根據題目的資料，設 ##AE=3k, ED=k, BM=MC=2k##。
由於 AMFE 是平行四邊形，所以 ##AE = MF##，因此 ##CF=k##。
let ##AE=3k, ED=k, BM=MC=2k##.
Since AMFE is a parallelogram, ##AE = MF##. Thus, ##CF=k##.

1) 證明 Prove DG = GC 
留意 △GDE ≅ △GCF (AAS)，
因此 DG = GC = 2k

2) 求 △BFG面積
留意 △BMH ~ △BFG (AAA) 

設 △BFG面積為 x。
Let the area of △BFG be x.

3) 求 k 
從 △BFG面積求 k的值。
Find the value of k from the area of △BFG.

$$\begin{align*}
\frac{(2k+2k+k)(2k)}{2} &= 25\\[2pt] \frac{(5k)(2k)}{2} &= 25\\[2pt] 5k^2 &= 25\\[2pt] k^2 &= 5\\
k &= \sqrt{5}
\end{align*}$$

4) 求 AEGH 面積

$$\begin{align*}
&\ AEGH\text{ 面積}\\
=&\ (4k)^2 -\color{blue}{\frac{(2k)(k)}{2}} -\color{green}{\frac{(4k)(2k)}{2}} -\color{red}{\frac{(2k)(4k)}{2}} +4\\[2pt] =&\ 16k^2 -\color{blue}{k^2} -\color{green}{4k^2} -\color{red}{4k^2} +4\\
=&\ 7k^2 +4\\
=&\ 7(5) +4\ \ (\because k^2=5)\\
=&\ 39\,\text{cm}^2
\end{align*}$$

留意 ∠ABD 是直角。
Note that ∠ABD is a right angle.

證明 Proof:

$$
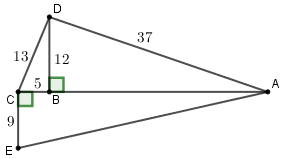\begin{align*}
AB^2 +BD^2 &= AD^2\\
AB^2 +12^2 &= 37^2\\
AB &= 35
\end{align*}$$ $$
\begin{align*}
AC^2 + CE^2 &= AE^2\\
(5+35)^2 + 9^2 &= AE^2\\
AE &= 41
\end{align*}$$ $$
\begin{align*}
&\ \text{周界 Perimeter}\\
=&\ 37 +13 +9 +41\\
=&\ 100\,\text{cm}
\end{align*}$$

參考下圖，加上兩條平行線。
Refer to the figure, construct two parallel lines.

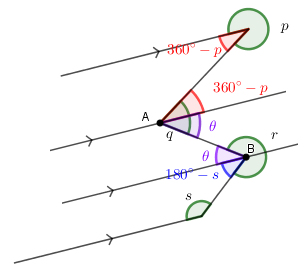
在 B 點，

在 A 點，

設 n 為多邊形的邊數
Let n be the number of side of the polygon.

$$\begin{align*}
(n -2)\times 180\deg &= 900\deg\\
n -2 &= 5\\
n &= 7
\end{align*}$$

I)
對角線數目 Number of Diagonals ##= C_2^7 -7=14##，所以選項 I 錯誤。

II)
Number of folds 折數 = 邊數 = 7，所以選項 II 正確。

III)
Number of axes 對稱軸數目 = 邊數 = 7，所以選項 III 正確。

相關文章：文憑試實戰篇 #7 多邊形性質

留意菱形亦即是4條邊長度相同的平行四邊形。其性質如下圖所示。
A rhombus is a parallelogram with four equal sides. The figure below shows its properties.

I)
∵∠DEC = ∠FCG = 90° 
∴DE//FC 

下圖所示的5隻角大小相同。
The 5 angles shown below are the same.

∠ADE = ∠EDI (Prop. of Rhombus 菱形性質) 
∠EDI = ∠ICF (alt. ∠s 錯角, DE//FC) 
∠ADE = ∠DEI (alt. ∠s 錯角, AD//EI) 
∠DEI = ∠IFC (alt. ∠s 錯角, DE//FC) 

∵∠IFC = ∠ICF 
∴CI = FI 

因此選項 I 正確。

II)

設 ∠ABE = x,
得到 ∠EBC = x, ∠BCE = 90° − x 

∠GCH = ∠BCE (vert. opp ∠s 對頂角) 
∴∠GCH = 90° − x, ∠ABE = x 

因此選項 II 並非必然正確。

III)
參考下圖，

∠DAE = ∠BCE (Prop. of Rhombus 菱形性質) 
∠CHF = ∠HCG (alt. ∠s 錯角, FH//CG) 
∴∠DAE = ∠CHF = 90° − x 

∠DEA = ∠CFH = 90° 

下一步是證明 DE = FC 

∠EDI = ∠IFC (Proved 已證) 
∠DEC = ∠FCE = 90° 
EC = CE (Common side 公共邊) 
∴△DEC ≅ △FCE (AAS) 

DE = FC 
∴△ADE ≅ △HCF (AAS) 

因此選項 III 正確。

AC 及 BE皆為圓的直徑，所以它們的交點為圓形的圓心。
Both AC and BE are diameters of the circle. So, their intersection is the centre of the circle.

設圓心為 O點。
Let the centre be point O.

∵OA = OB 
∴∠OAB = ∠OBA = 46° 

$$\begin{align*}
\color{red}{\angle POB} &= \color{green}{\angle OAB} +\color{green}{\angle OBA}\ \text{(Ext}\ \angle\ \text{of}\ \triangle\ \text{外角})\\
&= 46\deg +46\deg\\
&= 92\deg
\end{align*}$$ $$
\begin{align*}
\color{purple}{\angle APD} &= \color{red}{\angle POB} +\color{blue}{\angle PBO}\ \text{(Ext}\ \angle\ \text{of}\ \triangle\ \text{外角})\\
&= 92\deg +16\deg\\
&= 108\deg
\end{align*}$$

$$\begin{align*}
\tan \phi &= \frac{CD}{BC}\\[2pt] BC &= \frac{CD}{\tan \phi}\\[10pt] \sin \theta &= \frac{CD}{AD}\\[2pt] AD &= \frac{CD}{\sin \theta}
\end{align*}$$ $$
\begin{align*}
\frac{BC}{AD} &= \frac{\frac{CD}{\tan \phi}}{\frac{CD}{\sin \theta}}\\[2pt] &= \frac{CD}{\tan \phi} \times \frac{\sin \theta}{CD}\\[2pt] &= \frac{\sin \theta}{\tan \phi}
\end{align*}$$

$$U=(-3,-8)\\
V=(8,-3)\\
W=(-4,-3)$$

相關文章：文憑試實戰篇 #5 坐標旋轉 Rotation of Coordinates

方法一：
設 P = (h, k) 

把 (h, k) 代入 x − y + 13 = 0 
Put (h, k) into x − y + 13 = 0 
$$\begin{align*}
h -k +13 &= 0\\
h = k -13
\end{align*}\\
\ \\
\therefore P = (k -13,k)$$ $$\begin{align*}
AP &= PB\\
\sqrt{(k -13 +3)^2 + (k -1)^2} &= \sqrt{(k -13 +7)^2 + (k +5)^2}\\
(k -10)^2 + (k -1)^2 &= (k -6)^2 + (k +5)^2\\
k^2 -20k +100 +k^2 -2k +1 &= k^2 -12k +36 +k^2 +10k +25\\
-22k +101 &= -2k +61\\
40 &= 20k\\
k &= 2
\end{align*}$$

方法二：
由於 AP = PB，因此 P點在 AB 的垂直平分線上。
Since AP = PB, point P lies on the perpendicular bisector of AB.

設 M 點為 AB 的中點。
Let point M be the mid-point of AB.

$$\begin{align*} M&=\Big(\frac{-3 -7}{2},\frac{1 -5}{2}\Big)=(-5,-2)\\[8pt] m_{AB} &= \frac{1 +5}{-3 +7}\\[2pt] &=\frac{6}{4}\\[2pt] &=\frac{3}{2}
\end{align*}$$

設 m 為垂直平分線的斜率。
Let m be the slope of the perpendicular bisector.

$$\begin{align*}
m \times m_{AB} & = -1\\[2pt] m \times \frac{3}{2} &= -1\\
m &= \frac{-2}{3}
\end{align*}$$

AB 的垂直平分線 Perpendicular Bisector

解以下聯立方程 Solving the equations
$$\begin{cases}
2x +3y +16 =0\\
x -y +13 =0
\end{cases}\\
\ \\
P=(-11, 2)$$

 

兩條直線不相交，即是它們必定平行。
If two straight lines do not intersect, they must be parallel.

$$\begin{cases}
6x -8y = 7k\\
kx +12y = 5
\end{cases}\\
\begin{cases}
y = \frac{3}{4}x – \frac{7k}{8}\\
y = \frac{-k}{12}x +\frac{5}{12}
\end{cases}$$

它們的斜率相等
Their slopes are equal.
$$\begin{align*}
\frac{3}{4} &= \frac{-k}{12}\\[2pt] 36 &= -4k\\
k &= -9
\end{align*}$$

$$\begin{align*}
3x^2 +3y^2 -6x +12y -4 &= 0\\
x^2 +y^2 -2x +4y -\frac{4}{3} &= 0
\end{align*}$$ $$
\text{圓心 Centre}=(1, -2)\\
\begin{align*}
\text{半徑 radius} &= \sqrt{1^2 +2^2 +\frac{4}{3}}\\[2pt] &= \sqrt{\frac{19}{3}}\\
&\approx 2.52
\end{align*}$$

I)
方法一：
把 (0, 0) 代入圓形方程
Put (0, 0) into the equation of circle

因此選項 I 正確。

方法二：
原點與圓心的距離
The distance between the origin and centre

該距離小於半徑，因此原點在圓形之內。
The distance is shorter than the length of radius. Thus, the origin lies inside the circle.

因此選項 I 正確。

II)
$$\begin{align*}
\text{圓周 Circumference} &= 2\pi(2.52)\\
&\approx 15.8\\
&\lt 16
\end{align*}$$

因此選項 II 正確。

III)
參考下圖，

該距離 ##= 0-(-2) = 2## 

因此選項 III 正確。

所有組合數目 ##=C_2^6 = 15##
Number of Possible Combinations ##=C_2^6 = 15##

列出所有積不小於 12 的組合
List out all combinations whose products are not less than 12.
{2, 6}
{3, 4}
{3, 5}
{3, 6}
{4, 5}
{4, 6}
{5, 6} 

共有 7 種可能組合。
$$\therefore P = \frac{7}{15}$$

分佈域 Range = 472 −136 = 336 
四分位數間距 IQR = m −163 
$$\begin{align*}
336 &= 3\times(m -163)\\
112 &= m -163\\
m &= 275
\end{align*}$$

$$\begin{align*}
\frac{5 +5 +5 +6 +9 +9 +11 +13 +m +n}{10} &= 7\\
63 +m +n &= 70\\
m +n &=7
\end{align*}$$

因此 m 和 n 的值只有以下可能
{1, 6}
{2, 5}
{3, 4} 

I)
用計數機計算以上三種情況的標準差。
Calculate the standard deviations for all 3 possible cases with a calculator.

結果分別是 3.32, 3.19, 3.13。因此選項 I 正確。

II)
考慮以上三種情況，眾數都是 5。
The mode is 5 for all 3 possible cases.

因此選項 II 正確。

III)
計算以上三種情況的中位數
Calculate the median for all 3 possible cases.

結果分別是 6, 5.5, 5.5。因此選項 III 正確。

$$\begin{eqnarray}
& u^\color{red}{2} & v^3 & w^\color{red}{1} \\
& u^3 & v^\color{red}{1} & w^2 \\
& u^2 & v^3 & w^4 \\
\hline
\text{HCF}\ =\ & u^2 & v^1 & w^1\\
\end{eqnarray}$$

相關文章：文憑試實戰篇 #17 代數式的 HCF 及 LCM

$$\begin{align*}
&\text{AF000000000BC}_{16}\\
=&\color{green}{10 \times 16^{12} +15 \times 16^{11}} \color{blue}{+11 \times 16^1 + 12}\\
=&\color{green}{10 \times 16 \times 16^{11} +15 \times 16^{11}} \color{blue}{+188}\\
=&\color{green}{160 \times 16^{11} +15 \times 16^{11}} \color{blue}{+188}\\
=&\color{green}{175\times 16^{11}} \color{blue}{+188}
\end{align*}$$

相關文章：文憑試實戰篇 #18 再談二進制和十六進制數字

設 ##u= \log_2 y## 
$$\begin{cases}
x = u -2\\
u^2 = 5u +x -7
\end{cases}$$ $$\begin{align*}
\therefore u^2 &= 5u +(u -2) -7\\
u^2 -6u +9 &= 0\\
(u -3)^2 &= 0\\
u &=3\\
\ \\
\log_2 y &= 3\\
y &= 2^3\\
y &=8
\end{align*}$$

$$\text{斜率 slope} = \frac{0 -32}{2 -0} = -16$$參考 y − y₁ = m(x − x₁) 

相關文章：HKDSE 2018 數學科 Paper II Q33 題解

$$\begin{align*}
z &= (a -5)i +\frac{(a +2)i}{2 +i}\\[2pt] &= (a -5)i +\frac{(ai +2i)(2 -i)}{(2 +i)(2 -i)}\\[2pt] &= (a -5)i +\frac{2ai -ai^2 +4i -2i^2}{4 -i^2}\\[2pt] &= (a -5)i +\frac{2ai +a +4i +2}{4 +1}\ (\because i^2=-1)\\[2pt] &= (a -5)i +\frac{a +2 +(2a +4)i}{5}\\[2pt] &= \frac{a +2}{5} +(a -5)i + \frac{2a +4}{5}i
\end{align*}$$

∵ z 是實數 real number
$$\begin{align*}
(a -5)i + \frac{2a +4}{5}i &= 0\\
5a -25 + 2a +4 &= 0\\
7a -21 &= 0\\
a &= 3
\end{align*}$$ $$\begin{align*}
z &= \frac{a +2}{5}\\[2pt] z &= \frac{3 +2}{5}\\
z &= 1
\end{align*}\\
\ \\
a -z = 3 -1 =2$$

先用以上公式求取通項。
Find the general term with the formula.
$$\begin{align*}
T(n) &=S(n) -S(n -1)\\
&=n(2n +3) -(n -1)(2(n -1) +3)\\
&=2n^2 +3n -(n -1)(2n +1)\\
&=2n^2 +3n -(2n^2 +n -2n -1)\\
&=2n^2 +3n -2n^2 +n +1\\
&= 4n +1
\end{align*}$$

I)
$$\begin{align*}
T(n) = 4n +1 &= 14\\
4n &= 13\\
n &= \frac{13}{4}
\end{align*}$$

由於 n 不是整數，因此選項 I 錯誤。

II)
已知通項 General Term 是 4n + 1，因此選項 II 正確。

III)
$$\begin{align*}
T(n) &= 4n +1\\
&=4n -4 +4 +1\\
&=4(n -1) +5\\
&= 5 +(n -1)4
\end{align*}$$

因為通項能以 ##a +(n -1)d## 表示，因此該數列為等差數列。
Since the general term can be expressed as ##a +(n -1)d##, the sequence is an arithmetic sequence.

因此選項 III 正確。

Tips: 若 T(n) 能以 an + b 的方式表示，該數列便是等差數列 A.S.。

先作圖以瞭解各直線的位置。

 

透過聯立方程(Simultaneous Equations)，可找到 P, Q 及 R 點坐標。

P 點:

Q 點:

R 點:

然後把各點坐標代入 5x − 2y。

P: 5(1) −2(3) = −1 
Q: 5(−1) −2(−1) = −3 
R: 5(5) −2(2) = 21 

因此 5x − 2y 的最小值是 −3 
$$\begin{align*}
\color{blue}{5x -2y} +c &= 22\\
\color{blue}{-3} +c &= 22\\
c &= 25
\end{align*}$$

連接 CD 

$$\color{red}{\angle DCA }=\color{green}{ \angle TAD }= 55\deg \ (\angle\ in\ alt.\ segment\ \text{交錯弓形的圓周角})$$

在 BEDC,

在 △PCD,

設 ##u = \cos\theta## 
$$\begin{align*}
4u^2 -3u -1 &= 0\\
u =1\ \text{or}\ u &=-0.25
\end{align*}$$

當 ##\cos\theta = 1##,

當 ##\cos\theta = -0.25##,

所以共有3個根(roots)。

設 QS = 1 

$$\begin{align*}
\tan 30\deg &= \frac{QS}{QP}\\
\frac{1}{\sqrt{3}} &= \frac{1}{QP}\\
QP &= \sqrt{3}\\
\ \\
\sin 30\deg &= \frac{QS}{SP}\\
\frac{1}{2} &= \frac{1}{SP}\\[2pt] SP &= 2\\
\ \\
\tan 45\deg &= \frac{QS}{QR}\\[2pt] 1 &= \frac{1}{QR}\\[2pt] QR &= 1\\
\ \\
\sin 45\deg &= \frac{QS}{SR}\\[2pt] \frac{1}{\sqrt{2}} &= \frac{1}{SR}\\[2pt] SR &= \sqrt{2}
\end{align*}$$ $$
\begin{align*}
QR^2 + QP^2 &= PR^2\\
1^2 +(\sqrt{3})^2 &= PR^2\\
PR &= 2
\end{align*}$$

$$\begin{align*}
\cos \angle PRS &= \frac{SR^2 +PR^2 -SP^2}{2(SR)(PR)}\\
&= \frac{(\sqrt{2})^2 +2^2 -2^2}{2(\sqrt{2})(2)}\\
&= \frac{2}{4\sqrt{2}}\\
&= \frac{1}{2\sqrt{2}}\\
&= \frac{1\times \sqrt{2}}{2\sqrt{2}\times \sqrt{2}}\\
&=\frac{\sqrt{2}}{4}
\end{align*}$$

I)
形心必定在三角形之內。
Centroid must lie inside the triangle.

因此選項 I 正確。

II)
對於鈍角三角形，垂心位於三角形之外。
For obtuse triangles, the orthocentres lie outside the triangle.

因此選項 II 正確。

III)
留意該三角形為等腰三角形。紅色線是三角形的角平分線及垂直平分線。因此 I 點及 J 點都必定在紅色線上。而 Q 點並不在紅色線上。
Note that the triangle is an isosceles triangle. The red line is the angle bisector and perpendicular bisector of the triangle. Thus, point I and point J must lie on the red line. But point Q does not.

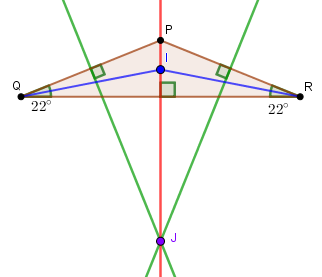
因此選項 III 錯誤。

所有可能排列數目 = 9! = 362880 

經理站在一起的排列數目 = 8! × 2! = 80640 

$$\begin{align*}
P(\text{答對最少一題}) &= 1 -P(\text{答對零題})\\
&= 1- (1 -0.6)(1 -0.7)(1 -0.8)\\
&= 0.976
\end{align*}$$

$$\text{standard score 標準分 }z=\frac{x-\mu}{\sigma}$$##\mu## = mean 平均值
##\sigma## = standard deviation 標準差

$$z=\frac{x-\mu}{\sigma}$$##z## = standard score 標準分
##\mu## = mean 平均值
##\sigma## = standard deviation 標準差

I)
把各考試分數由小至大排列。
Arrange the scores in ascending order.

中位數 median ##=\frac{25 +26}{2} = 25.5## 

因此選項 I 錯誤。

II)
用計數機得到

平均值 mean = 23.75, 標準差 standard deviation = 8.35 

$$\begin{align*}
z &= \frac{x -\mu}{\sigma}\\
2 &= \frac{x -23.75}{8.35}\\
x &= 40.45
\end{align*}$$

所有分數都小於 40.45，因此選項 II 正確。

III)
標準差 standard deviation = 8.35，因此選項 III 正確。

方差 Variance = (標準差 Standard Deviation)²

在每個數據乘上相同的常數 k。
  Standard Deviation 標準差為原來的 k倍。

在每個數據加上相同的常數

  標準差並無改變。
  Standard deviation does not change.

Standard Deviation 標準差 ##=\sqrt{16} \times 9 = 36##