等腰梯形性質 (Isosceles Trapezium)
等腰三角形大家必定非常熟悉,但等腰梯形就很少接觸了。現在就一同認識它的性質。
定義
如下圖所示,兩條腰(斜邊)長度相等的梯形,就是等腰梯形(isosceles trapezium)。
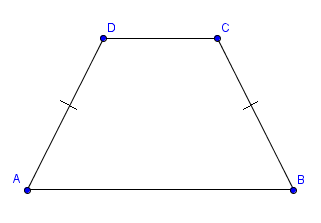
性質
等腰梯形有兩個性質要特別留意:
1) 反射對稱

用日常用語來說就是「左右對稱」。 由此可推斷:
- ∠A = ∠B
- ∠C = ∠D
- AC = BD
- ΔAKD ≅ ΔBKC
- ΔADB ≅ ΔBCA
- ΔACD ≅ ΔBDC
2) 對角和 = 180°
從平行線性質得知,
∠A + ∠D = 180° (int ∠s, AB//CD) ∵∠C = ∠D∴∠A + ∠C = 180°
由於對角和 = 180°,因此等腰梯形是圓內接四邊形 (Cyclic Quadrilateral)。
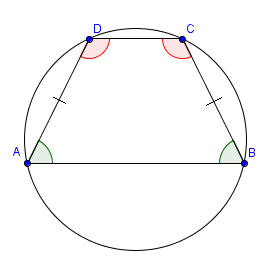
判定
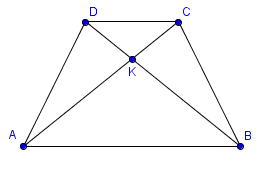
以下任何一個條件皆可判定等腰梯形。
1) AD = BC (腰線長度相等)
2) ∠DAB = ∠CBA (底角相等)
3) ∠ADC = ∠BCD (頂角相等)
4) AC = BD (對角線長度相等)
特別留意第4項,這項並不顯而易見。
相關試題
- 2005P2Q26
分類: 幾何、坐標及三角學



感謝您寶貴的資料!
don’t know what you are talking about .
don’t know wt you are talking ab.mmnnj
bruh