消失了的課程 ─ 弧度 radian
大家都知道計數機上的 D 字如果被設定成 R 或 G，所有三角函數的計算結果將會改變。那麼 R 和 G 到底是什麼呢?
弧度 radian 是什麼?
弧度 radian 是角大小的量度單位。就如量度線段的長度時，我們可以用 cm 來量度，亦可以用英吋來量度。而弧度就是「角度」 degree 以外另一量度角大小的單位。而計數機上的 R 就是 radian 的意思。
角度和弧度之間以下列公式作轉換，亦即是一隻直角的孤度是 ##\large \frac{\pi }{2}##。
π rad = 180°
為什麼要採用弧度 radian?
採用弧度來量度角的大小可以把一些數學公式簡化。
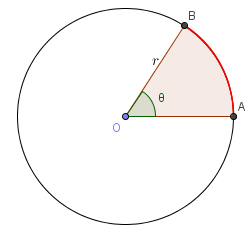
參考上圖，AB 的弧長 arc length 用以下公式求取：
$$\overset{\displaystyle\frown}{AB} = 2 \pi r \times \frac{\theta}{360^{\circ}}$$
但如果 θ 以弧度表示，分母的 360° 亦須改用弧度表示，即是 2π rad。因此
$$\begin{align*}
\overset{\displaystyle\frown}{AB} &= 2 \pi r \times \frac{\theta}{2\pi}\\
&= r \theta
\end{align*}$$
\overset{\displaystyle\frown}{AB} &= 2 \pi r \times \frac{\theta}{2\pi}\\
&= r \theta
\end{align*}$$
而扇形 Sector OAB 的面積亦可簡化成:
$$\text{Area of OAB} = \frac{1}{2} r^2 \theta$$
弧度 radian 在微積分中亦擔當重要的角色。在處理微積分時所有角的值均以孤度表示。
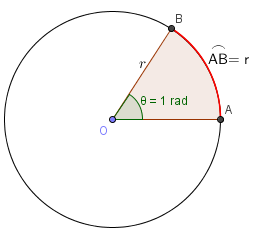
當 θ = 1 rad
留意弧長的公式，當圓心角 = 1 rad 時，
$$\begin{align*}
\overset{\displaystyle\frown}{AB} &= r (1)\\
&= r
\end{align*}$$
\overset{\displaystyle\frown}{AB} &= r (1)\\
&= r
\end{align*}$$
即是弧長等於半徑長度。所以弧度的另一演繹是弧長和半徑長度之比 (ratio between arc length and radius)。
弧度 radian 的單位
弧度的維度 (dimension) 是 0 。換句話說，弧度並沒有單位。但有時為了避免混淆，所以加上 rad 作為標示。而 rad 並非必要。所以同學寫出角度時， 絕對不可以遺漏「°」這符號，否則別人會把這數值當作弧度看待。
總結
弧度是角度以外另一個量度角大小的單位，而一隻直角 = ##\large \frac{\pi}{2}## rad。而弧度在數學世界中擔當極重要的角色。
分類: 幾何、坐標及三角學
發表回應