HKDSE 2012 Practice Paper Maths Paper II 題解
HKDSE 2012 Practice Paper Maths Paper II Answers and Solutions
香港中學文憑考試 2012 練習卷 數學卷二答案+題解。
試題可從考評局網頁下載,連結:
資料來源:香港考試及評核局網頁
$$\begin{align*}
&\ x^3(2x+x)\\
=&\ x^3(3x)\\
=&\ 3x^4
\end{align*}$$
$$\begin{align*}
3a + 1 &= 3(b -2)\\
3a + 1 &= 3b\ -6\\
3a + 7 &= 3b\\
b &= \frac{3a}{3} + \frac{7}{3}\\
b &= a + \frac{7}{3}\\
\end{align*}$$
$$\begin{align*}
&\ p^2 -q^2 -p -q\\
=&\ (p^2 -q^2) -(p + q)\\
=&\ (p -q)(p + q) -(p + q)\\
=&\ (p + q) (p -q -1)
\end{align*}$$
$$\begin{align*}
m(x -3)^2 + n(x+1)^2 \equiv &\ x^2 -38x +41\\
m(x^2 -6x +9) + n(x^2 +2x +1) \equiv &\ x^2 -38x +41\\
mx^2 -6mx +9m +nx^2 +2nx + n \equiv &\ x^2 -38x +41\\
(m+n)x^2 +(-6m+2n)x + 9m +n \equiv &\ x^2 -38x +41
\end{align*}$$
Comparing the coefficients,
比較係數
$$\begin{cases}
m+n = 1\\
-6m+2n = -38\\
9m +n = 41
\end{cases}$$
Solving the equation,
解聯立方程
$$m= 5, n=-4$$
方法二:
對於恆等式,x 是任何數值,該等式均成立。
Since it is an identity, the equality is always true regardless of values of x.
When x=−1,
$$\begin{align*}
m(-1 -3)^2 + n(-1 +1)^2 = &\ (-1)^2 -38(-1) +41\\
m(-4)^2 = &\ 80\\
16m = &\ 80\\
m = &\ 5
\end{align*}$$
$$\begin{align*}
&\ \text{remainder 餘數}\\
=&\ f(-2)\\
=&\ (-2)^4 -(-2)^3 +(-2)^2 -(-2) +1\\
=&\ 31
\end{align*}$$
$$\begin{align*}
\Delta &= 0\\
(2k)^2 -4(3)(-k) &= 0\\
4k^2 +12k &=0\\
k^2 +3k &=0
\end{align*}$$
$$k =0\ \ \text{or}\ \ k=-3$$
I) 很明顯這選項正確
II)
$$\begin{align*}
\text{slope 斜率} &= \frac{3-0}{0-5}\\[3pt]
&=\frac{-3}{5}
\end{align*}$$
∴ 選項 II 錯誤
III) L3的方程為 y = 3,因此選項 III 正確。
II) b 為曲線的 截距 y-intercept 而從圖得知 b 是負數。因此選項 II 正確。
III) 從圖像得知方程有兩個不等實根 (two unequal real roots),
$$\begin{align*}
\Delta &\gt 0\\
(-2)^2 -4(a)(b) &\gt 0\\
4 -4ab &\gt 0\\
-4ab &\gt -4\\
ab &\lt 1
\end{align*}$$
因此選項 III 正確。
相關文章:文憑試實戰篇#3 圖像和係數的關係
4x \gt x -3\ \ &\text{or}\ \ 3 -x \lt x +7\\
3x \gt -3\ \ &\text{or}\ \ -x -x\lt +7-3\\
x \gt -1 \ \ &\text{or}\ \ -2x \lt 4\\
x \gt -1 \ \ &\text{or}\ \ x \gt -2\\
\end{align*}$$
$$\therefore x \gt -2$$
Selling Price = Cost × (1 + Profit%)
售價 = 成本 × (1 + 利潤%)
Selling price of John's vase
偉明的花瓶的售價
##\begin{align*}
=&\ 1600 \times (1+20\%)\\
=&\ 1920\end{align*}##
Selling price of Susan's vase
素珊的花瓶的售價
##\begin{align*}
=&\ 1920\times (1+20\%)\\
=&\ 2304\end{align*}##
如果 C 增加 40%,r 同樣增加 40%。
New area 新面積
##\begin{align*}
=&\ \pi (1.4r)^2\\
=&\ 1.96 \pi r^2
\end{align*}##
Percentage Increase 百份數增加
##\begin{align*}
=&\ \frac{1.96 \pi r^2 -\pi r^2}{\pi r^2} \times 100\%\\
=&\ 96\%
\end{align*}##
\frac{\alpha +\beta}{3\alpha -\beta} &= \frac{7}{3}\\[3pt] 3\alpha + 3\beta &= 21\alpha -7\beta\\[3pt] 10\beta &= 18\alpha\\[3pt] \frac{10}{18} &= \frac{\alpha}{\beta}\\[3pt] \frac{\alpha}{\beta} &= \frac{5}{9}
\end{align*}$$
z &= \frac{kx}{y^2}\\
\frac{y^2z}{x} &= k\\
k &= \frac{y^2z}{x}\\
\frac{1}{k} &= \frac{x}{y^2z}
\end{align*}$$
註: 等式右方是 ##\large \frac{1}{k}##,只要當中不涉及任何變數(如 x,y,z),它就是常數 constant。
A. 0.009 (correct to 3 decimal place)
C. 0.009050 (correct to 6 decimal place)
D. 0.00905000 (correct to 6 significant figures)
相關文章:為什麼小數最左手面的零並非有效數字?
$$\begin{align*}
\frac{r \times r}{2} &= 12\\
r^2 &=24
\end{align*}$$
Area of Segment ABC
弓形面積
##=\pi r^2 \times \frac{1}{4} -12\\[3pt]
=\pi (24) \times \frac{1}{4} -12\\[3pt]
=6\pi -12\\
=6(\pi -2)\text{ cm}^2##
設 r 為半徑
$$\begin{align*}
r^2 + 8^2 &= 17^2\\
r &= 15
\end{align*}$$
$$\begin{align*}
&\text{Volume 體積}\\
=&\ \frac{1}{3} \pi r^2 h\\
=&\ \frac{1}{3} \pi 15^2 (8)\\
=&\ 600\pi\text{ cm}^3
\end{align*}$$
根據題目所提供的資料,可找到以下的邊長。
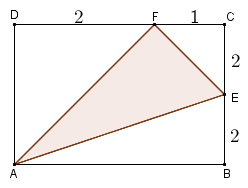
$$\begin{align*}
&\ \text{Area 面積} \\
=&\ (3 \times 4) -\frac{2 \times 4}{2} -\frac{2 \times 3}{2} -1\\
=&\ 4\text{ cm}^2
\end{align*}$$
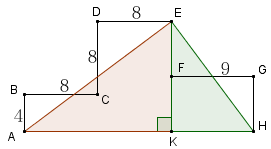
In △AEK,
$$\begin{align*}
AE &= \sqrt{AK^2 + EK^2}\\
&= \sqrt{ (8 +8)^2 +(4 +8)^2}\\
&= \sqrt{400}\\
&=20
\end{align*}$$
In △HEK,
$$\begin{align*}
HE &= \sqrt{HK^2 +EK^2}\\
&= \sqrt{ (9)^2 +(4 +8)^2}\\
&= \sqrt{225}\\
&=15
\end{align*}$$
$$\begin{align*}
&\ \text{Perimeter 周界}\\
=&\ AE +HE +AH\\
=&\ 20 +15 +(8 +8 +9)\\
=&\ 60\text{ cm}
\end{align*}$$
在下圖中,相同顏色的角的大小相同。

$$\begin{align*}
\angle BCE &= 180\deg -64\deg -64\deg\ (\because AB//CE)\\
&=52 \deg
\end{align*}$$
$$\begin{align*}
\angle CDE &= 180\deg -52\deg -52\deg\\
&=76 \deg
\end{align*}$$

參考圖像,留意以下各點:
- ##\angle ADB = 90\deg##
- ##\angle OKB = \angle ADB = 90\deg## (##\because AD//OC##)
- 設 ##\angle BAC = \theta##,則 ##\angle COB = 2\theta##
In △OKB,
$$\begin{align*}
2 \theta +90\deg +24\deg &= 180\deg\\
\theta = 33\deg
\end{align*}$$
In △AEB,
$$\begin{align*}
\angle AED &= \angle EAB + \angle EBA\\
&= 33\deg +24\deg\\
&= 57\deg
\end{align*}$$
已知 ##\large\frac{a}{x} = \frac{b}{y} = \frac{c}{z}##,則 ##a:b:c = x:y:z##
$$\begin{eqnarray*}
\overset{\displaystyle\frown}{AB} &= \overset{\displaystyle\frown}{BC} &= 2\overset{\displaystyle\frown}{CD}\\[3pt]
\frac{\overset{\displaystyle\frown}{AB}}{2} &= \frac{\overset{\displaystyle\frown}{BC}}{2} &= \frac{\overset{\displaystyle\frown}{2CD}}{2}\\[3pt]
\frac{\overset{\displaystyle\frown}{AB}}{2} &= \frac{\overset{\displaystyle\frown}{BC}}{2} &= \frac{\overset{\displaystyle\frown}{CD}}{1}
\end{eqnarray*}$$
即是 ##\overset{\displaystyle\frown}{AB}:\overset{\displaystyle\frown}{BC}:\overset{\displaystyle\frown}{CD} = 2 :2 :1 ##
Referring to the figure, join OB and OC.
參考圖像,把 OB 及 OC 連接

設 Let ∠AOB = ∠BOC = 2θ and ∠COD = θ,
$$\begin{align*}
2\theta + 2\theta + \theta + 70\deg &= 360\deg\\
5\theta &= 290\deg\\
\theta &= 58\deg
\end{align*}$$
$$\begin{align*}
\angle BCD &= \frac{1}{2} \angle BOD\\[3pt]
&= \frac{1}{2} (2 \times 58\deg + 70\deg)\\[3pt]
&= 93\deg
\end{align*}$$
Step 1) Find ∠ABE.

$$\begin{align*}
\because AB &= AE\\[3pt]
\therefore \angle ABE &= \frac{180\deg -112\deg}{2}\\
&= 34\deg
\end{align*}$$
Step 2) 證明 ∠FCD=34°。
有很多方法可證明 ∠FCD=34°,以下是其中一個方法。
設 Let ∠FCD=α, ∠ABF = β.
參考以下圖像,

$$\angle CFG = \angle FCD = \alpha\\
\angle GFB = \angle ABF = \beta$$
##\because CF//BE##
$$\begin{align*}
\therefore \angle CFB &= \angle FBE\\
\alpha + \beta &= \beta + 34\deg\\
\alpha &= 34\deg
\end{align*}$$
Step 3) Find CF and BF.

Let the length of the sides of the square be 1.
設正方形邊長為 1。
$$\begin{align*}
\cos 34\deg &=\frac{CD}{CF}\\[3pt]
\cos 34\deg &=\frac{1}{CF}\\[3pt]
CF &= \frac{1}{\cos 34\deg}\\[3pt]
&= 1.2062
\end{align*}$$
##\text{In }\triangle CFB##,
$$\begin{align*}
\cos 56\deg &= \frac{CF^2 +BC^2 -BF^2}{2\cdot CF \cdot BC}\\[3pt]
&= \frac{1.2062^2 +1^2 -BF^2}{2\cdot 1.2062 \cdot 1}\\[3pt]
BF &= 1.05163
\end{align*}$$
Step 4) Find ∠ABF.
##\text{In }\triangle ABF##,
$$\begin{align*}
\cos \angle ABF &= \frac{AB}{BF}\\[3pt]
&= \frac{1}{1.05163}\\[3pt]
\angle ABF &= 18.0\deg\\
&\approx 18\deg
\end{align*}$$
&\ \frac{30}{3\sin^2\theta+2\sin^2(90\deg -\theta)}\\
=&\ \frac{30}{3\sin^2\theta+2\cos^2\theta}\\[1pt] =&\ \frac{30}{3\sin^2\theta+2(1-\sin^2\theta)}\\[1pt] =&\ \frac{30}{\sin^2\theta+2}
\end{align*}$$
當分母是最大值時,該數式的數值最小。
When ##\sin^2\theta = 1##,
$$\begin{align*}
&\ \frac{30}{\sin^2\theta+2}\\[1pt]
=&\ \frac{30}{1+2}\\
=&\ 10
\end{align*}$$
選項 I 及 II 很明顯正確。
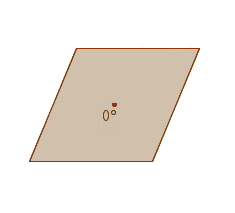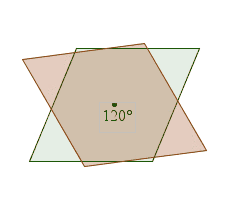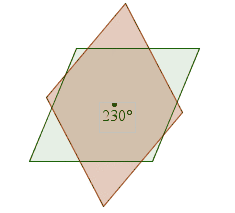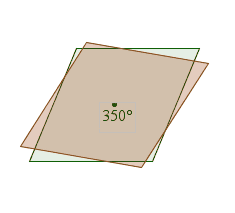
而選項 III 的平行四邊形的四條邊長相同,即是它是一個菱形 rhombus。
參考下圖,它擁有兩條反射對稱軸 axis of reflectional symmetry。而且當它旋轉 180° 後,如原圖形重疊,因此它同時擁有反射對稱軸 reflectional symmetry 及旋轉對稱 rotational symmetry 性質。


設 P 點坐標為 (h,k)。
由於 P 點在 ##y = x +2## 之上,
##\therefore k = h +2 ##
$$\begin{align*}
AP &= PB\\
\sqrt{(1 -h)^2 + (-3 -k)^2} &= \sqrt{(-5 -h)^2 + (7 -k)^2}\\
(1 -h)^2 + [-3 -(h+2)]^2 &= (-5 -h)^2 + [7 -(h+2)]^2\\
(1 -h)^2 + (-5 -h)^2 &= (-5 -h)^2 + (5 -h)^2\\
(1 -h)^2 &= (5 -h)^2\\
1 -2h +h^2 &= 25 -10h +h^2\\
8h &= 24\\
h &= 3
\end{align*}$$
$$\begin{align*}
k &= (3) +2\\
&=5
\end{align*}$$
##\therefore P = (3,5)##
相關文章:當某點在一直線上
$$\begin{align*}
2x^2 +2y^2 +8x -12y +3 &=0\\
x^2 +y^2 +4x -6y +\frac{3}{2} &=0\\
\end{align*}$$
I) 圓心坐標 = (−2, 3),所以選項 I 正確。
II)
$$\begin{align*}
&\ \text{radius 半徑}\\
=&\ \sqrt{ (2)^2 + (3^2) -\frac{3}{2}}\\
=&\ 3.39
\end{align*}$$
∴選項 II 錯誤。
III)
distance between (2,3) and the centre
(2,3) 與圓心的距離
##=\sqrt{(2+2)^2 + (3-3)^2}\\
= 4\\
\gt \text{radius }半\,徑##
∴該點在圓形之外,即是選項 III 正確。
(3,5) (5,3)
(5,7) (7,5)
$$\begin{align*}
P &= \frac{1}{4} \times \frac{1}{3} \times 4\\[3pt]
&= \frac{1}{3}
\end{align*}$$
I) 最高的學生的高度是 185cm,因此選項 I 錯誤。
II) IQR = 180−165 = 15cm ,因此選項 II 正確。
III) 中位數 median = 175cm,因此選項 III 錯誤。
I) ##m_1## 及 ##m_2## 的值可從下圖所示的方法找到。因此選項 I 錯誤。

II) ##r_1## 及 ##r_2## 的值可從下圖所示的方法找到。因此選項 II 正確。
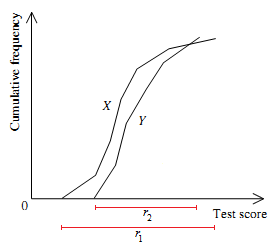
III) 標準差 standard deviation 的值無法直接從圖像得到。但由於選項 I 錯誤,因此可判斷答案是 C。
$$g(x) = 2f(x)$$
According to transformation of function, ##f(x)## is enlarged along y-axis 2 times.
根據函數變換,意思是把 ##f(x)## 沿 y 軸放大兩倍。
因此答案是 D。
方法二:
根據題目的圖像,可得到以下的等式。
$$\begin{cases}
f(2)=0\\
f(6)=0\\
f(0)=-2
\end{cases}$$
由於 ##g(x) = 2f(x)##,可得到
$$\begin{cases}
g(2)=0\\
g(6)=0\\
g(0)=-4
\end{cases}$$
觀察各選項,只有選項 D 的圖像符合以上的等式。因此答案是 D。

$$\begin{align*}
&\ \text{B0000000023}_{16}\\
=&\ 11\times 16^{10} + 2 \times 16^1 + 3 \times 16^0\\
=&\ 11\times 16^{10} + 32 + 3\\
=&\ 11\times 16^{10} + 35
\end{align*}$$
##a^3 +b^3 = (a +b) (a^2 -ab + b^2)##
##a^2 +b^2 = (a+b)^2 -2ab##
$$\begin{align*}
\alpha + \beta &= k\\
\alpha \times \beta &= 3
\end{align*}$$
$$\begin{align*}
&\ \alpha^3 +\beta^3\\[2pt]
=&\ (\alpha +\beta) (\alpha^2 -\alpha\beta +\beta^2)\\[2pt]
=&\ (\alpha +\beta) (\alpha^2 +\beta^2 -\alpha\beta)\\[2pt]
=&\ (\alpha +\beta) [(\alpha +\beta)^2 -2\alpha\beta -\alpha\beta]\\[2pt]
=&\ (\alpha +\beta) [(\alpha +\beta)^2 -3\alpha\beta]\\[2pt]
=&\ k [k^2 -3(3)]\\[2pt]
=&\ k^3 -9k
\end{align*}$$
&\ (x +3i)(3 +i)\\
=&\ 3x +xi +9i +3i^2\\
=&\ 3x +xi +9i -3\ \ (\because i^2 = -1)\\
=&\ 3x -3 + xi +9i
\end{align*}$$
Real Part 實部 = ##3x -3##
The general term of the sequence is ##2n +3##. It means it is an arithmetic sequence.
數列的通項是 ##2n+3##,代表它是等差數列。
$$\begin{align*}
a &= T(1)\\
&= 2(1) +3\\
&= 5
\end{align*}$$
$$\begin{align*}
d &= T(2) -T(1)\\
&= [2(2) +3] -5\\
&= 2
\end{align*}$$
$$\begin{align*}
S(m) &= 3000\\
\frac{m}{2}[(2a+(m -1)d] &= 3000\\
\frac{m}{2}[(2(5)+(m -1)2] &= 3000\\
\frac{m}{2}(10+2m -2) &= 3000\\
m(10+2m -2) &= 6000\\[3pt]
8m +2m^2 -6000 &= 0\\[3pt]
m^2 +4m -3000 &= 0\\[3pt]
m=-56.8\text{ or }m=52.8
\end{align*}$$
∴ m 的最大值是 52。
註:原則上應運用 ##S(m) \lt 3000##,來找 ##m## 的範圍,但以等式(##S(m)=3000##) 處理會較簡單。
##\log_a b = \large \frac{\log b}{\log a}##
$$\begin{align*}
\ \ \ a &= \log_{12} b\\[3pt]
a &= \frac{\log b}{\log 12}\\[3pt]
\frac{1}{a} &= \frac{\log 12}{\log b}\\[3pt]
\frac{1}{a} &= \log_b 12
\end{align*}$$
$$\begin{align*}
\log_3t&=0&\ \log_3x&=-4\\
t&=3^0& x&=3^{-4}\\
t&=1& x&=\frac{1}{81}
\end{align*}$$
把 ##t=0, x=\frac{1}{81}## 代入 ##x=kt^a##。
$$\begin{align*}
x &= kt^a\\[2pt]
\frac{1}{81} &= k\cdot (1)^a\\
k &= \frac{1}{81}
\end{align*}$$
相關文章:HKDSE 2014 Paper I Q15 題解
方法二:
由於 (135°, 2) 在曲線上,所以可把 x=135° 代入方程右方,並把各選項的數值代入 a 及 θ,並測試其值是否等於 2。
A) ##-2\sin(135\deg -45\deg) = -2##
B) ##-2\sin(135\deg +45\deg) = 0##
C) ##2\sin(135\deg -45\deg) = \color{red}{2}##
D) ##2\sin(135\deg +45\deg) = 0##
∴選項 C 是正確答案。

參考圖像,當 k 保持不變而 h 增加時,θ 的值下降。
根據題目的資料,可得到
##AE \lt GF \lt GE\\[4pt] \therefore a \gt c \gt d##
註: 小心不要被圖像的視差所誤導,由於 ##AG:GB=5:3##,所以很明顯 ##GE \gt GF##。
相關文章:文憑試實戰篇 #19 斜面上的直線的斜率
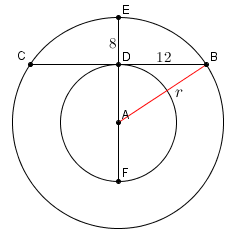
參考圖像,設大圓半徑為 r。
##\text{In }\triangle ABD,##
$$\begin{align*}
AD^2 + BD^2 &= AB^2\\
(r-8)^2 + 12^2 &= r^2\\
r^2 -16r +64 + 144 &= r^2\\
r &=13
\end{align*}$$
$$\begin{align*}
AD &= AE -ED\\
&= 13 -8\\
&= 5
\end{align*}$$
$$\begin{align*}
EF &= ED + AD \times 2\\
&= 8 + 5 \times 2\\
&= 18
\end{align*}$$
x^2 +y^2 +6x +ky -k = 0\ …(1)\\
x -y =0\ …(2)
\end{cases}$$
把 ##y=x## 代入 (1),
$$\begin{align*}
x^2 +x^2 +6x +kx -k = 0\\
2x^2 +6x +kx -k = 0\\
\end{align*}$$
Since the straight line does not intersect with the circle,
由於直線和圓不相交,
$$\begin{align*}
\Delta &\lt 0\\
(6+k)^2 -4(2)(-k) &\lt 0\\
36 +12k +k^2 +8k &\lt 0\\
k^2 +20k +36 &\lt 0\\
(k+18)(k+2) &\lt 0\\
-18 \lt k &\lt -2
\end{align*}$$
 x 軸是 AB 的高線 Altitude,因此垂心 Orthocentre 必定在 x軸之上,亦即是其 y坐標為 0。
x 軸是 AB 的高線 Altitude,因此垂心 Orthocentre 必定在 x軸之上,亦即是其 y坐標為 0。設垂心坐標為 H(h,0),基於垂心性質。
$$\begin{align*}
m_{BH} \times m_{OA} &= -1\\[3pt]
\frac{0+24}{h -18} \times \frac{24-0}{18-0} &= -1\\[3pt]
\frac{24}{h -18} \times \frac{4}{3} &= -1\\[3pt]
\frac{24}{h -18} &= \frac{-3}{4}\\[3pt]
96 &= -3h +54\\[2pt]
3h &= -42\\[2pt]
h &= -14
\end{align*}$$

P &= \frac{9!}{10!}\\[3pt] &= \frac{1}{10}
\end{align*}$$
設 ##x_i##是原有數字。
New number 新數
##=(x_i +5) \times 3\\
= 3x_i +15##
換句話說,即是把各數字乘 3,然後加上 15。
New mean 新平均值 ##= 3 \times 40 + 15 = 135##
New variance 新方差 ##= 9 \times 3^2 = 81##
New inter-quartile range 新四分位數間距 ##= 18 \times 3 = 54##
I)
原本的中位數 original median ##=\large \frac{\beta +\gamma}{2}##
新的中位數 new median ##=\mu + 2##
無法判斷那一個數較大,因此選項 I 並非必定正確。
II)
原本的分佈域 original range ##=\delta -\alpha##
新的分佈域 new range ##=(\delta +2) -(\alpha+2) =\delta -\alpha##
因此選項 II 正確。
III) 由於 μ 是較接近原有數據的平均值 mean,因此把它加入後可降低標準差 standard deviation。即是選項 III 正確。
註:選項 III 較難判斷是否正確,但由於選項 I 並非必定正確,因此答案是 C。
分類: 計數機應用及歷屆試題



發表回應